Для наглядности последовательность этапов МАИ проиллюстрируем на примере выбора метода решения нелинейного уравнения.
1.1. Постановка задачи
Из множества известных методов решения нелинейных уравнений выбрать метод решения, обеспечивающий наилучшие оценки в соответствии с МАИ. Следует отметить, что необходимую информацию о содержании и особенностях методов решения нелинейных уравнений студенты получили при изучении дисциплины «Численные методы».
1.2. Построение иерархии
Одним из основных принципов построения МАИ является принцип идентичности и декомпозиции, который предусматривает структурирование проблем в виде иерархии или сети, что является первым этапом МАИ. На рисунке 1 представлен наиболее общий вид иерархии, которая строится с вершины (целей – с точки зрения управления), через промежуточные уровни (критерии, от которых зависят последующие уровни,) к самому низкому уровню (который обычно является перечнем альтернатив).
Иерархия считается полной, если каждый элемент данного уровня функционирует как критерий для всех элементов нижестоящего уровня.
В результате реализации первого этапа МАИ любая, сколь угодно сложная проблема, может быть представлена в виде трехуровневой иерархии (цель – критерии – альтернативы), каждый из элементов иерархии при необходимости может быть представлен, в свою очередь, в виде трехуровневой иерархии и т.д.
Структурирование проблемы осуществляют участники процесса решения (например, группа экспертов или ЛПР). При структурировании представленной в п.1.1 задачи в качестве эксперта была привлечена старший преподаватель кафедры кибернетики и вычислительной техники, к.т.н. Козлова Е.В., читающая дисциплину «Численные методы». Для построения полной простой иерархии, представленной на рисунке 2, были определены цель, критерии и альтернативы.
Целью задачи принятия решения в данном примере является выбор наиболее эффективного метода решения нелинейных уравнений. Альтернативами выбора являются следующие методы:
М1. Метод половинного деления;
М2. Метод простой итерации;
М3. Метод Ньютона-Рафсона (классический);
М4. Метод секущих.
В результате обсуждения для дальнейшего рассмотрения был отобран следующий список из пяти критериев (обозначим их буквой «А» с соответствующим номером):
А1. Скорость сходимости метода;
А2. Вычислительная сложность алгоритма решения;
А3. Шаговость метода;
А4. Зависимость числа итераций при получении решения от расположения точки начального приближения;
А5. Гарантия сходимости.
1.3. Принцип дискриминации и сравнительных суждений
Цель второго этапа МАИ – установить приоритеты критериев и оценить каждую из альтернатив по критериям, выявив самую важную из них.
1.3.1. Попарные сравнения
В МАИ элементы одного уровня иерархии сравниваются попарно по отношению к их воздействию («весу» или «интенсивности») на общую для них характеристику. Например, строится матрица для сравнения относительной важности критериев на втором уровне по отношению к общей цели на первом уровне. Подобные матрицы должны быть построены для попарных сравнений каждой альтернативы на третьем уровне по отношению к критериям второго уровня.
Пусть А1, А2,…, Аn – элементы одного уровня иерархии. При проведении попарных сравнений в основном ставятся следующие вопросы относительно элементов элементов Аi и Аk:
- какой из них важнее или имеет большее воздействие?
- какой из них более вероятен?
- какой из них предпочтительнее?
При этом каждому субъективному суждению необходимо дать количественную оценку, пользуясь шкалой относительной важности. Количественные оценки, вводимые при попарных сравнениях, строят исходя из некоторых эмпирических правил, опирающихся на основание опыта.
При любом подходе к разрешению задачи сравнения важное значение имеет выбор шкалы сравнений. Главное требование - шкала сравнений должна быть проста и естественна.
Так как единица является стандартом измерения, то верхняя граница должна быть не слишком далека от нее, хотя и достаточно отдалена для того, чтобы более или менее выразительно представить наш диапазон способности различать. Поэтому и число сравниваемых объектов должно быть достаточно мало. Обычные пределы - это 7 ± 2 единиц.
Опишем один из способов того, как практически придать количественное наполнение сравнению объектов, действий или обстоятельств. В таблице 1 представлена в общем виде матрица попарных сравнений (матрица А).
Таблица 1- Общий вид матрицы попарных сравнений
| A1 | А2 | Аk | An | |||
| A1 | а11 | а12 | а1k | a1n | ||
| А2 | а21 | а22 | а2k | a2n | ||
| Аi | аi1 | аi2 | аik | ain | ||
| Аn | аn1 | an2 | ank | ann |
Пусть даны элементы А1, А2, и т. д. Матрица попарных сравнений размером n×n строится по следующим правилам:
- если элементы Аi и Ak одинаково важны, заносим в позиции (Аi, Ak) и (Ak, Аi) матрицы число 1,
- если элемент Аi незначительно важнее элемента Ak, заносим в позицию (Аi, Ak) число 3, а в позицию (Ak, Аi) – обратное ему число 1/3;
- если элемент Аi значительно важнее элемента Ak, заносим в позицию (Аi, Ak) число 5, а в позицию (Ak, Аi) – обратное ему число 1/5;
- если элемент Аi явно важнее элемента Ak, заносим в позицию (Аi, Ak) число 7, а в позицию (Ak, Аi) – обратное ему число 1/7;
- если элемент Аi по своей значимости абсолютно превосходит элемент Ak, заносим в позицию (Аi, Ak) число 9, а в позицию (Ak, Аi) – обратное ему число 1/9.
Числа 2, 4, 6 и 8 используются для облегчения компромиссов между оценками, слегка отличающимися от основных чисел.
Таким образом, мы получаем таблицу сравнений, которой соответствует обратносимметричная матрица размером n×n. Поскольку элемент Аi находится в отношении безразличия к самому себе, все элементы главной диагонали матрицы попарных сравнений имеют значения, равные единице.
1.3.2. Построение матрицы попарных сравнений второго уровня. Решение и согласованность
В нашем примере второй уровень иерархии содержит пять критериев (матрица размером 5×5 представлена таблицей 2). Каким образом элементы матрицы получили свои значения? Эксперту был задан вопрос: «При выборе метода решения нелинейных уравнений какой критерий является более значимым – Скорость сходимости метода (А1) или Вычислительная сложность алгоритма решения (А2)?». Был получен ответ «Скорость сходимости метода». Затем эксперту был задан вопрос: «Насколько важнее критерий А1 относительно критерия А2?». Был получен ответ: «Незначительно важнее». В результате элементу матрицы (A1, А2) присвоено значение 3, а элементу матрицы (A2, А1) – обратное значение 1/3. Аналогично были проведены остальные попарные сравнения.
Таблица 2 - Матрица попарных сравнений второго уровня
| Критерий | А1 | А2 | А3 | А4 | А5 | |
| А1 | Скорость сходимости метода | 1 | 3 | 1 | 2 | 1/3 |
| А2 | Вычислительная сложность алгоритма решения | 1/3 | 1 | 1 | 1/2 | 1/2 |
| А3 | Шаговость метода | 1 | 1 | 1 | 1 | 1/3 |
| А4 | Зависимость числа итераций при получении решения от расположения точки начального приближения | 1/2 | 2 | 1 | 1 | 1/3 |
| А5 | Гарантия сходимости | 3 | 2 | 3 | 3 | 1 |
Общее число попарных сравнений, которые необходимо провести, вычисляется по формуле
1.3.3. Вычисление вектора приоритетов для матрицы попарных сравнений второго уровня
Из группы матриц попарных сравнений формируется набор локальных приоритетов, которые выражают относительное влияние множества элементов на элемент примыкающего сверху уровня. Находят относительную силу (величину, ценность, желательность или вероятность каждого отдельного объекта) через «решение» матриц, каждая из которых обладает обратносимметричными свойствами. Для этого нужно вычислить множество собственных векторов для каждой матрицы, а затем нормализовать результат к единице, получая тем самым вектор приоритетов.
Вычисление оценки компонент собственного вектора можно произвести различными способами, например, сначала вычислить геометрическое среднее в каждой строке матрицы А по формуле
Полученный по формуле (1) столбец чисел нормализуется делением каждого числа ![]() на сумму B всех чисел столбца, в результате получаем значения компонент вектора локальных приоритетов (3).
на сумму B всех чисел столбца, в результате получаем значения компонент вектора локальных приоритетов (3).
Так как числа ![]() нормализуются делением каждого числа на сумму всех чисел, очевидно
нормализуются делением каждого числа на сумму всех чисел, очевидно
Проведем вычисления компонент вектора локальных приоритетов для нашего примера (вычисления будем проводить с точностью до четвертого знака):
Просуммируем полученные значения:
Далее воспользуемся формулой (2):
Проведем проверку по формуле (3):
Очевидно, погрешность вычислений компонент вектора локальных приоритетов для матрицы попарных сравнений второго уровня равна нулю. Если же условие (3) не выполняется, необходимо оценить погрешность вычислений по следующей формуле:
Анализ результатов этапа вычисления вектора приоритетов для матрицы попарных сравнений второго уровня. Полученные значения компонент ![]() вектора локальных приоритетов критериев дают возможность ранжировать критерии в соответствии с предпочтениями ЛПР по убыванию полученных весов. Для рассматриваемого примера в таблице 3 критерии распределены в соответствии с «занятыми местами». Для ЛПР самым весомым является критерий «Гарантия сходимости», который «выигрывает» у ближайшего «преследователя» - критерия «Скорость сходимости метода»
вектора локальных приоритетов критериев дают возможность ранжировать критерии в соответствии с предпочтениями ЛПР по убыванию полученных весов. Для рассматриваемого примера в таблице 3 критерии распределены в соответствии с «занятыми местами». Для ЛПР самым весомым является критерий «Гарантия сходимости», который «выигрывает» у ближайшего «преследователя» - критерия «Скорость сходимости метода»
Таблица 3 – Численные оценки предпочтений критериев ЛПР
| Критерий | Место | Вес | |
| А5 | Гарантия сходимости | 1 | 0,3977 |
| А1 | Скорость сходимости метода | 2 | 0,2057 |
| А3 | Шаговость метода | 3 | 0,1438 |
| А4 | Зависимость числа итераций при получении решения от расположения точки начального приближения | 3 | 0,1438 |
| А2 | Вычислительная сложность алгоритма решения | 5 | 0,1090 |
Значение критерия, получившего самую низкую оценку («Вычислительная сложность алгоритма решения»), по мнению ЛПР, не является пренебрежимо малым, так как его вес составляет 10,9% от суммарного веса всех критериев. В противном случае критерии с пренебрежимо малыми весами следует исключить из рассмотрения и повторить п.п. 1.3.2 и 1.3.3. Критерии «Шаговость метода» и «Зависимость числа итераций…» получили по формуле (2) одинаковые значения весов и «разделили» третье место.

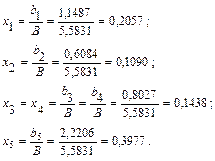
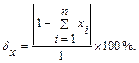
0 коммент.:
Отправить комментарий